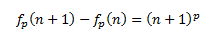I did this calculation manually the first time through—some years ago. It goes a lot easier with a computer algebra system. Today, I'm going to use Maxima to solve the problem.
An identity which comes up in the development of the complex numbers, gives a convenient way of expressing \(\sin {n\theta}\) in terms of combinations of \(\sin \theta\) and \(\cos \theta\).
De Moivre's formula:
\[r^n (\cos \theta + i \sin \theta)^n = r^n (\cos {n\theta} + i \sin {n\theta}).\]
So, if we take \(r=1\) and \(n=5\), we can do a binomial expansion and easily isolate the \(sin \theta\) and \(\cos \theta\). In a Maxima cell, I type
eq: (cos(%theta) + %i*sin(%theta))^5 = cos(5*%theta) + %i*sin(5*%theta);
realpart(eq);
imagpart(eq);
After executing, I obtain the fifth angle identities (if you want to call them that).
\[\mathrm{cos}\left( 5\,\theta\right) =5\,\mathrm{cos}\left( \theta\right) \,{\mathrm{sin}\left( \theta\right) }^{4}-10\,{\mathrm{cos}\left( \theta\right) }^{3}\,{\mathrm{sin}\left( \theta\right) }^{2}+{\mathrm{cos}\left( \theta\right) }^{5}\]
\[\mathrm{sin}\left( 5\,\theta\right) ={\mathrm{sin}\left( \theta\right) }^{5}-10\,{\mathrm{cos}\left( \theta\right) }^{2}\,{\mathrm{sin}\left( \theta\right) }^{3}+5\,{\mathrm{cos}\left( \theta\right) }^{4}\,\mathrm{sin}\left( \theta\right) \]
To eliminate \(\cos^2 \theta\) from the sine identity we use
subst([cos(%theta)=sqrt(1-sin(%theta)^2)],%);
expand(%);
and obtain
\[\mathrm{sin}\left( 5\,\theta\right) =16\,{\mathrm{sin}\left( \theta\right) }^{5}-20\,{\mathrm{sin}\left( \theta\right) }^{3}+5\,\mathrm{sin}\left( \theta\right). \]
Taking \(\theta=18°\), using \(x\) to stand in for \(\sin 18°\), and rearranging, we have
\[0 = 16\,{x}^{5}-20\,{x}^{3}+5\,x - 1.\]
Factoring this one manually was made easier by recognizing \(x = 1\) as a root. After that I tried forming a square free polynomial and found that there was in fact a squared polynomial involved. In general, this helps in a couple ways (potentially):
- Reduces the degree of the polynomial to be factored.
- Sometimes produces fully reduced factors as a by-product of forming the square free polynomial.
- This happens when each repeated factor is of different degree; that is, occurs a different number of times.
(Square free means no factors left that are raised to some power—each factor occurs exactly once.) Doing this manually involves taking the greatest common divisor between a polynomial and it's derivative. But today, let's let Maxima do it.
factor(0=16*x^5-20*x^3+5*x - 1);
\[0=\left( x-1\right) \,{\left( 4\,{x}^{2}+2\,x-1\right) }^{2}.\]
At this point, you really do have to be exceedingly lazy to not continue with the rest of the work manually. It's just a quadratic formula to be applied now (we discard \(x=1\) as an artifact). To use a computer algebra system for the rest is...well...okay, it is Saturday [at original publication], so...
solve(0=4*x^2+2*x-1,[x]);
\[[x=-\frac{\sqrt{5}+1}{4},x=\frac{\sqrt{5}-1}{4}]\]
We reject the negative solution (which is \(\sin {-54°}\) and, interestingly, is the negative of half the Fibonacci number) on the grounds that the range of the sine function on our interval is positive. Hence,
\[\sin 18° = \frac {\sqrt{5} - 1}{4}.\]